The diagrams in Figure 9 illustrate net forces and moments for trim attitude balanced symmetrical, unstable, and stable airfoils respectively. All airfoil forces and moments are in balance separately such that, when drag forces are neglected, the lift force equals but opposes the gravitational force and the camber line induced pitching moment equals but opposes moments resulting from offset between center of gravity and aerodynamic center.
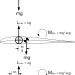
All airfoil lift forces are directed through the aerodynamic center (ac) located at the 25% point of mean chord. Symmetrical airfoils have straight camber lines and, consequently, generate no moments and the CG force vector is in line and opposes the lift vector as shown in the diagram. Lift and CG forces for cambered airfoils are also equal and opposite but are offset horizontally from one another. That horizontal separation develops a moment equal in magnitude but opposite in direction to the camber line induced moment. As a consequence, the CG position offset from ac is linked to the airfoil camber line characteristics. If the CG is forward of ac, the airfoil is stable, has a positive cm, and a reflex camber line. If the CG is aft of ac, the airfoil is unstable, has a negative cm, and a positive camber line. If the CG is at the ac, the airfoil is symmetrical, has a zero cm, and a straight camber line.
With CG position remaining fixed, the wing pitching moment can simply be manipulated with control of airfoil camber line or cm and the elevon is the obvious control surface to use. Proportional nose up and down pitching moments can be produced with up and down elevon deflections of measured magnitude. This then provides a convenient means to control the wing pitch attitude with respect to wing trim attitude or wing angle of attack.
As with conventional tailed airplanes, the flying wing plank can be trimmed over a range of angles of attack. But fixing the trim angle of attack also fixes the CG position in a way which is dependent on the cm for the selected airfoil. The relationship between the three variables, the angle of attack (in terms of cl), the airfoil camber line (in terms of cm), and the CG position (in terms of xn) is defined by the following simple but interesting equation.
cm/cl = xn (1)
where xn is the CG position forward of aerodynamic center of the mean chord as a fraction of the mean chord. See Figure 10 for definition of xn.
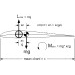
Per the equation there is a tradeoff between trim cl and CG position for a fixed airfoil cm. For example, lets assume the wing airfoil is the MH32, cm = -0.057. From the equation, xn = -0.057/cl. Based on the polar for the MH32, with a comfortable trim cl selection of 0.8, xn = -0.057/0.8 = -0.07, or a CG at 32% of mean chord.
Another interesting consequence of the way the active pitch stabilizer functions is that it provides an automatic flap feature at no extra cost (see Figure 11). Recall that the elevator control signal is also merged with the AOA sensor signal to control the elevon. Intuition suggests that the elevon moves up with up elevator control inputs. Initially this is true, but as the airspeed decreases, cl increases to maintain constant lift and as a result the elevon actually begins to lower to below trim angle since the ratio cm/cl has to remain constant per equation (1). This is so because the CG remains fixed. Similarly, with down elevator control inputs the elevon will eventually move up providing some reflex camber as the flight speed increases in order to satisfy equation (1). This is exactly the correct response for best performance as we saw from the discussion in the “Airfoil Performance Concepts”, Figure 11.



